So I this tweet early morning and was intrigued by this tweet. Had no idea what a Lugn algorithm and vigenere cipher was and had forgotten about caesar cipher. Its as good as a day to start learning as any other day, so I decided to code these things up.

Luhn Algorithm

So essentially this algorithm was created by an IBM scientist Hans Peter Luhn. Its also called the mod 10 algorithm. It essentially works out to check for errors in digits of IMEI or credit card number and so on. It is not an algorithm against malicious attacks, it just something that is used to ensure accidental error while typing card number. If you try to pay by credit card and after typing it out if there is a mistake there then it says you have typed the wrong credit number.

This is a fake American express card number I took from https://developers.bluesnap.com/reference/test-credit-cards.

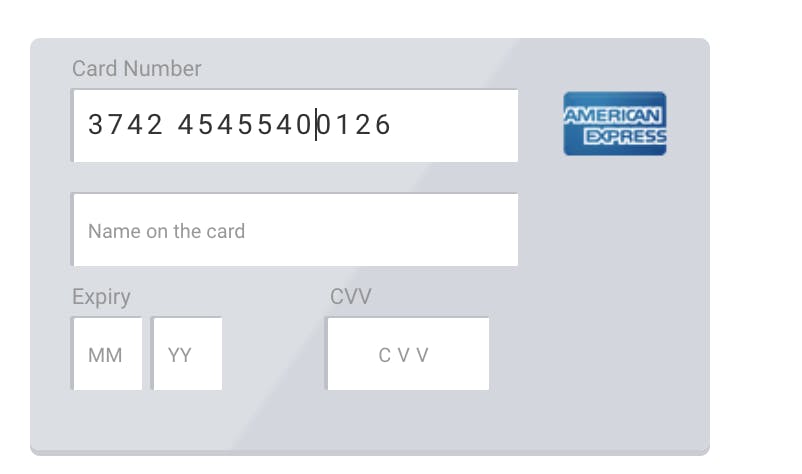
Now if I change one of the number in this:

How does Luhn work

Let me take the same 374245455400126 as the example credit card number.

• Starting from the rightmost digit, start doubling every second digit

• 

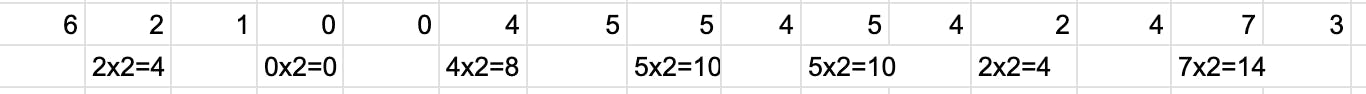
• If after a sum the value is greater than 9, then sum the digits(this can also be done by just subtracting by 9 which is easier in code)

  

• Sum all the values now

  

• The sum has to be a multiple of 10, which is the case here.

python code for Luhn

def luhn(number):
    sum = 0
    card_number = str(number)
    is__num_len_even = len(card_number)%2==0
    for i, digit in enumerate(card_number):
        digit = int(digit)
        # this is because we are enummerating from first digit from left
        # and if length is even then when we start from the rightmost digit
        # we end the first digit from left, if len is off we end up at the 
        # second digit from left.
        if(i%2==(0 if is__num_len_even else 1)):
            digit*=2
            if digit>9:
                digit-=9
        sum+=digit
    return sum%10==0
print(luhn(374245455400126))

Caesar cipher

Caesar cipher is an encoding scheme where we shift the letters in a phrase by a fixed number for all. A cipher with fixed number as 3 would shift A to D, C to F and so on. As it seems like from the name, it is attributed to Julius Caesar itself, it is said that he used this cipher to share information with his generals. The cipher said to be used had a fixed number of 3. It is also said that Augustus used this as well with 1 as the fixed number, the difference being that instead of wrapping around at end, in the sense that A for Z, they used AA instead.

Of course given there are only 26 letters so only 25 different ways of encoding, brute force is usually enough to break the cipher. Although when it was prominent this method was not as feasible making it harder to crack.

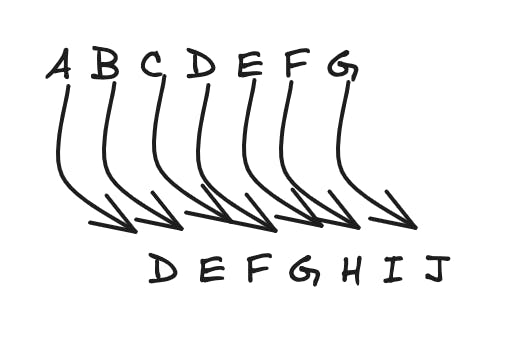
Example ciphering

Assuming a fixed number of 3, this is how caesar cipher would shift it to different letters.

How to code this

def caesar_encrypt(text, shift):
    result = ""
    for char in text:
        if char.isalpha():
            # we have to do all this calculation is because we need the shit to wrap around
            # when character is "x" and we need to shit it by 3, it should be "a" but if we do
            # not use the modulo calculation to wrap around we will "{"" instead 
            base = ord('a') if char.islower() else ord('A')
            result += chr((ord(char) - base + shift)%26 + base)
        else:
            result+=char
    return result

def caesar_decrypt(text, shift):
    return caesar_encrypt(text, -shift)


text = "Hello, World!"
shift = 3
encrypted_text = caesar_encrypt(text, shift)
decrypted_text = caesar_decrypt(encrypted_text, shift)

print("Original:", text)
print("Encrypted:", encrypted_text)
print("Decrypted:", decrypted_text)

Vigenère cipher

This is another type of method to encrypt data, in this we choose a keyword whatever that might be and shift the each letter of keyword based on corresponding letter of the text. A Vigenère table is generally used to do this:

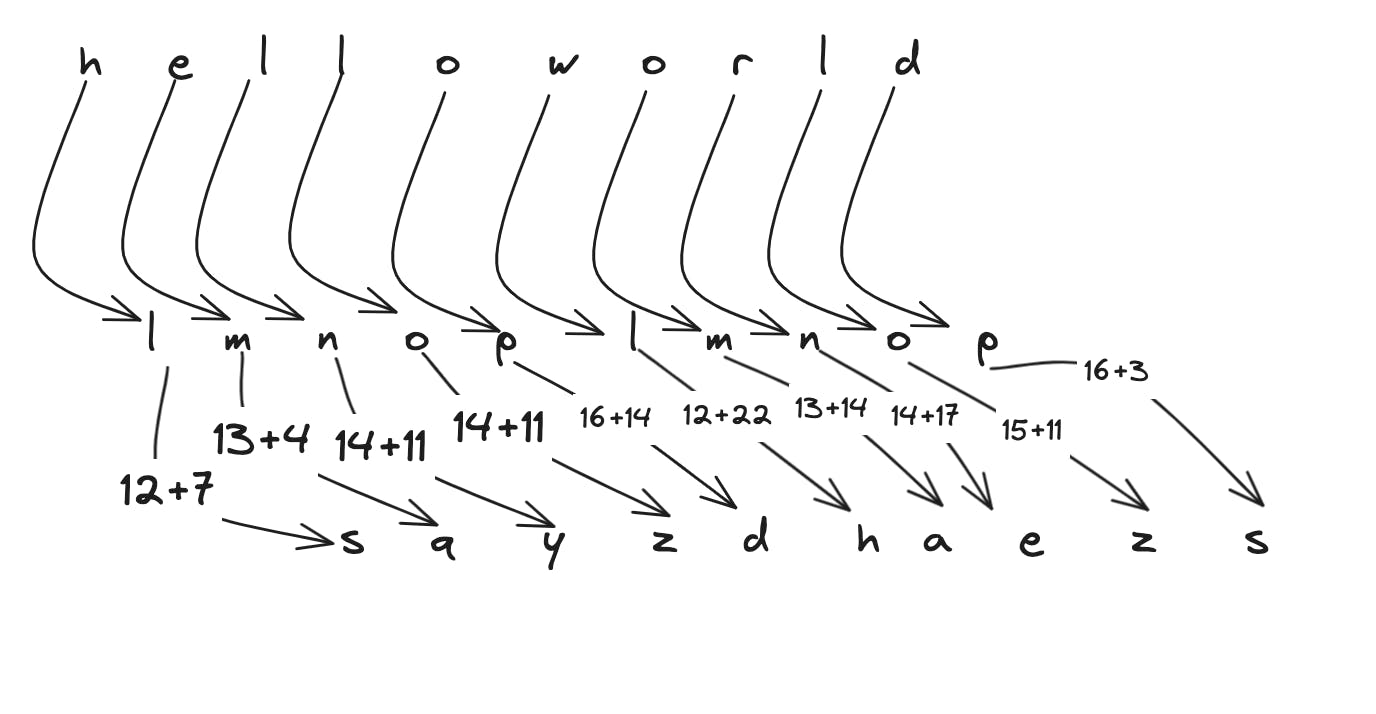
There are of courses cases where the keyword is shorter than the text, in that case we keep repeating the keyword until it matches the length of the text. For instance if the text is "hello world" and the keyword is "lmnop" then we keep repeating "lmnop" until it matches, so in this case that would be "lmnoplmnop". If we take a look at the table, the other way of looking at this is we shift the keyword with the ordinal value of letter in text subtracted by one. So ordinal value of 'h' is 7, so we shift 'l' by 7 so it should become 's'.

Example cipher

Code

def vigenere_cipher(text, keyword, decrypt=False):
    result = ""
    keyword = keyword.upper()
    key_index = 0
    for char in text:
        if char.isalpha():
            key = ord(keyword[key_index % len(keyword)]) - ord('A')
            base = ord('a') if char.islower() else ord('A')
            shift = key if not decrypt else -key
            result += chr((ord(char) - base + shift) % 26 + base)
            key_index += 1
        else:
            result += char
    return result

# Example usage
text = "Hello World"
keyword = "lmnop"
encrypted_text = vigenere_cipher(text, keyword)
decrypted_text = vigenere_cipher(encrypted_text, keyword, decrypt=True)

print("Original:", text)
print("Encrypted:", encrypted_text)
print("Decrypted:", decrypted_text)