TIL but from tweets(I am the guy who can't implement breadth first search without googling)

Of course I cannot implement BFS without googling lol, not the smartest or sharpest but I can write an article about it though.

What is BFS?

BFS is a graph traversal algorithm to find the shortest path for two points in a graph. Many of the problems in computer science and life can be represented as graphs and can be solved using graph algorithms. In BFS we go through the vertices in the present depth level and only after traversing them all, goes to the next level. This definition feels nice and all but what does a level mean, what does going to the next level, essentially in a given graph we first traverse the nodes that one 1 edge away, then 2 edge away and so on. So we traverse all the nodes that are "y" edges away before traversing through points that are "y+1" distance.

How does graph traversal in BFS happen?

So we start by adding the first node into a queue and mark it as visited. Then remove the node from the queue and start visiting neighbours. For each unvisited neighbour, we add it to the queue and mark it as visited. We need to mark the nodes as visited, this is because of the nature of the graph where there might be cycles and you probably will be coming back to the same node multiple times, which we dont want.

Example traversal

• Push 1 into queue and mark it as visited

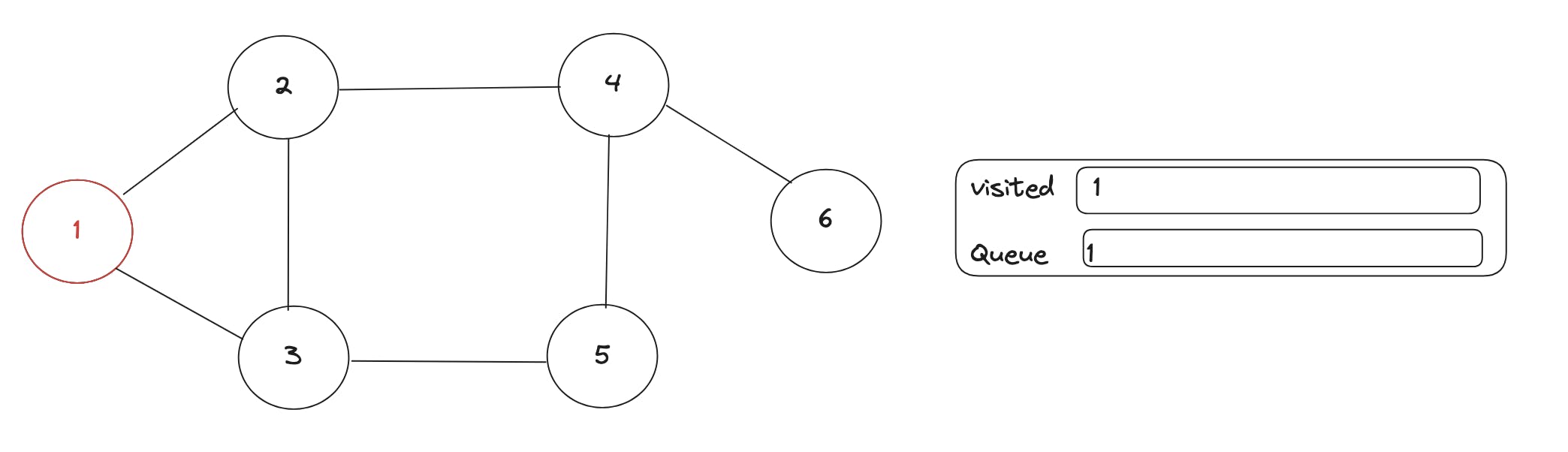
• Remove 1 and visit its neighbours and add them to the queue, in this case 2 and

  

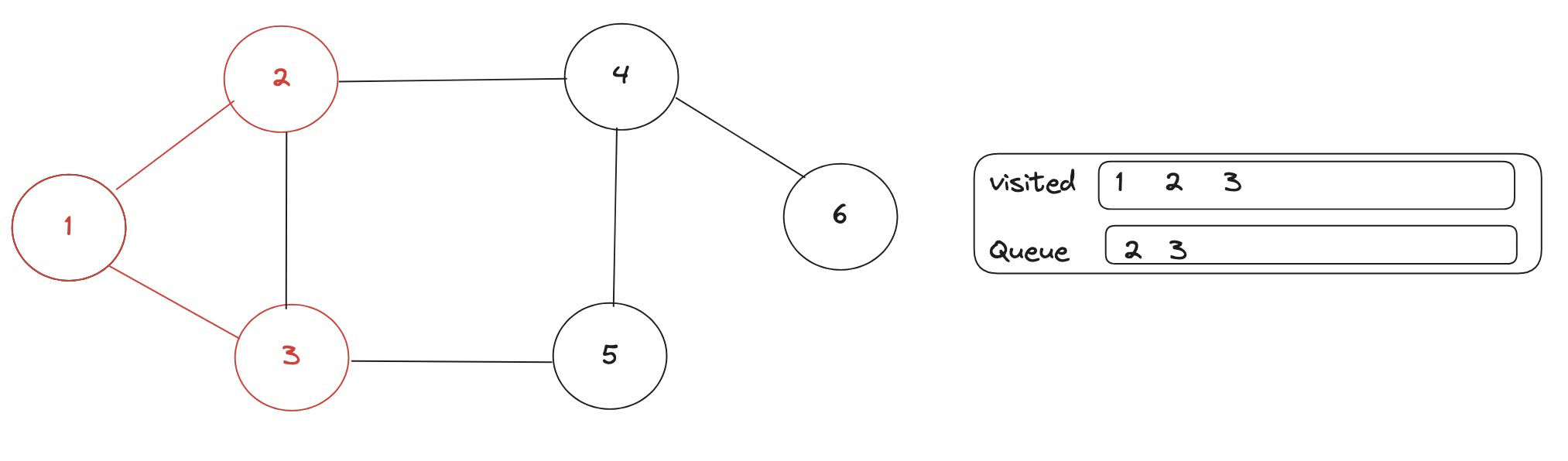
• Then we start 2 with, remove it from the queue and then visits its neighbours and add them to the queue, here they are 3 and 4 but 3 has already been visited, so only 4 is added to the queue

  

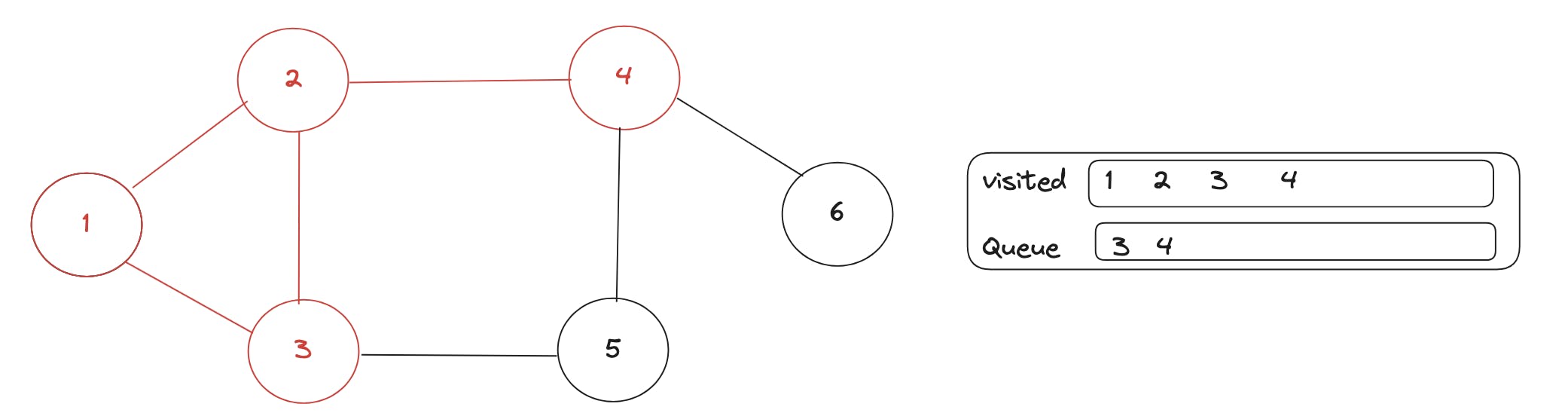
• Now we on and traverse through neighbours of 3, remove it from the queue, visit its unvisted neighbours, mark them visited, in this case 2 is already visited, so only 5 and add 5 to the queue

  

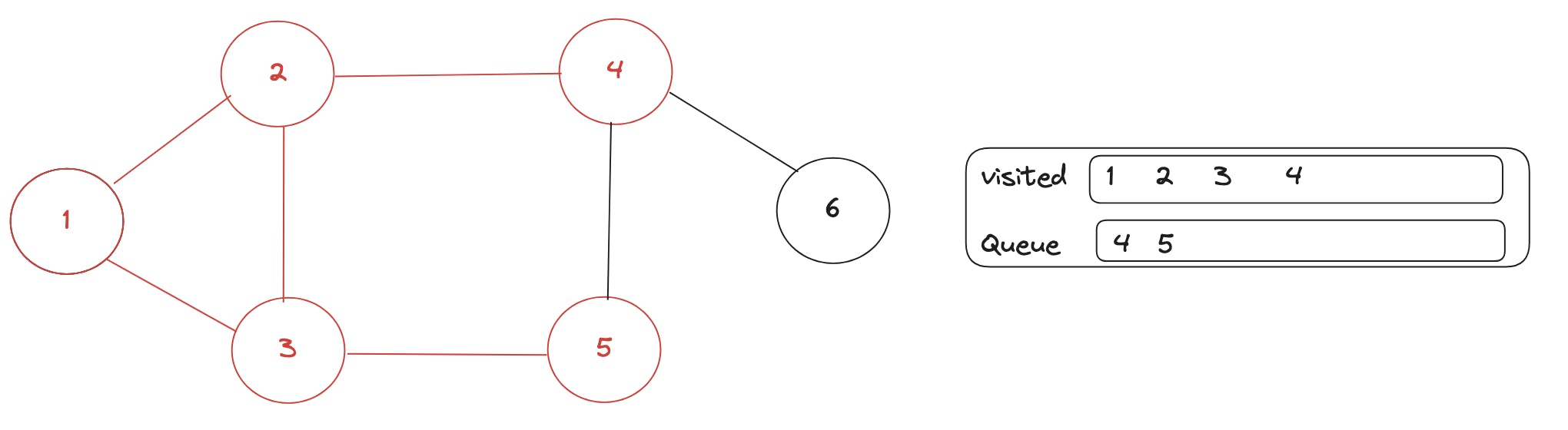
• With start point as 4 now, remove 4 from the queue, add unvisited neighbours to the queue and mark them visited, here 2, 5 already visited, so only 6 is added to the queue

  

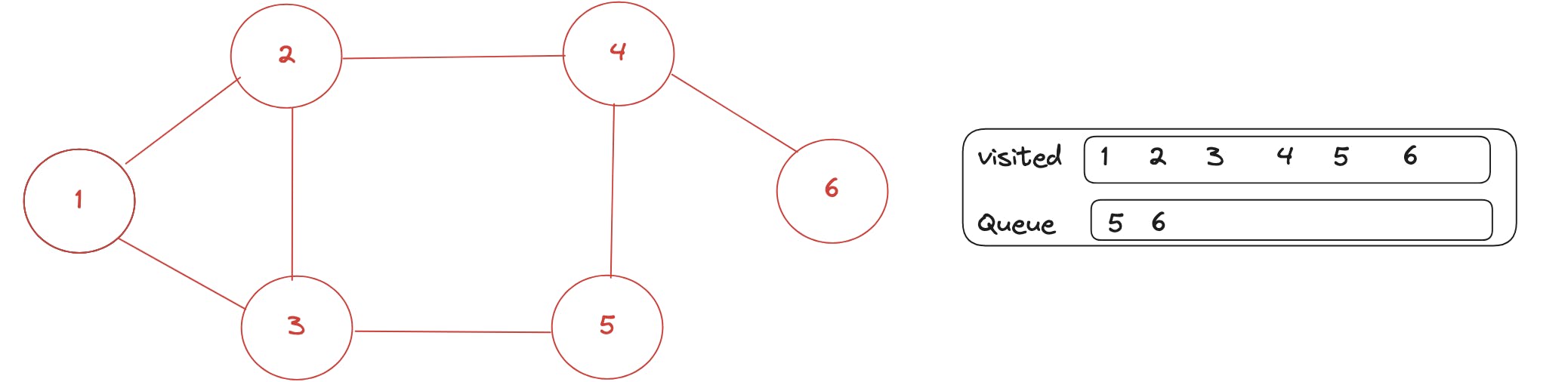
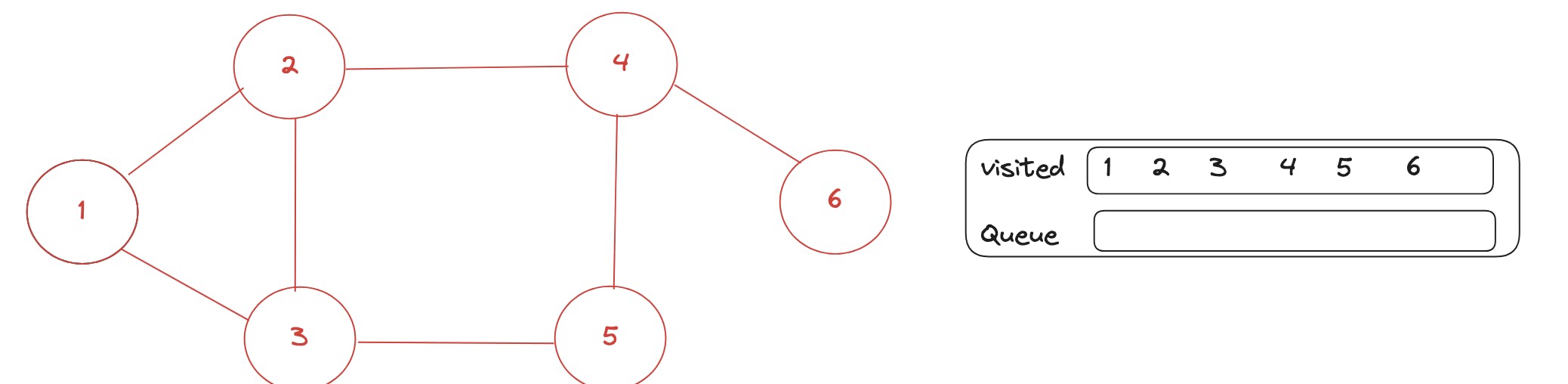
• Now next for 5 and 6 which are in the queue, no new unvisited neighbours present, so we just remove them from the queue that's all

  

Just code it

pseudocode

BFS(graph, start_vertex):
    // Create a queue to hold vertices to visit
    queue = Queue()
    // Add the starting vertex to the queue
    queue.enqueue(start_vertex)
    // Mark the starting vertex as visited
    visited[start_vertex] = true

    while not queue.is_empty():
        // Remove the vertex at the front of the queue
        current_vertex = queue.dequeue()
        // Print the current vertex
        print(current_vertex)

        // Iterate over the neighbors of the current vertex
        for neighbor in graph.get_neighbors(current_vertex):
            // If the neighbor has not been visited
            if not visited[neighbor]:
                // Add the neighbor to the queue
                queue.enqueue(neighbor)
                // Mark the neighbor as visited
                visited[neighbor] = true

codeeeeee

So before we code there are two types of graph that might need solving with bfs one is adjacency list and adjacency matrix, algorithm for both is same only, just code will slightly change that's all.

def bfs(graph, start):
    # create a queue
    queue = []
    # enqueue it with start index and mark it as visited
    queue.append(start)
    visited = {start}
    while queue:
        # dequeue the vertex
        removed_vertext = queue.pop(0)
        print(f"Current vertext {removed_vertext}")

        # get all neighbours of dequeued vertex and if not visited
        # add it too the queue and mark it as visited
        for neighbour in graph[removed_vertext]:
            if neighbour not in visited:
                queue.append(neighbour)
                visited.add(neighbour)

# Example graph represented as an adjacency list
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

# Perform BFS starting from vertex 'A'
bfs(graph, 'A')

def bfs(graph, start):
    # create graph
    G = []
    # enqueue the start and mark it as visited
    G.append(start)
    visited = [False]*len(graph)
    visited[start] = True

    while G:
        # remove the first vertex and print it
        removed_vertext = G.pop(0)
        print(f"Current vertex {removed_vertext}")

        # get all neighbours of the removex vertex and if not visited
        # add them to queue and mark as visited
        for i in range(len(graph[removed_vertext])):
            if graph[removed_vertext][i] == 1 and not visited[i]:
                G.append(i)
                visited[i] = True

# Example graph represented as an adjacency matrix
graph = [
    [0, 1, 1, 0, 0, 0],  # A
    [1, 0, 0, 1, 1, 0],  # B
    [1, 0, 0, 0, 0, 1],  # C
    [0, 1, 0, 0, 0, 0],  # D
    [0, 1, 0, 0, 0, 1],  # E
    [0, 0, 1, 0, 1, 0]   # F
]

# Perform BFS starting from vertex 0 (A)
bfs(graph, 0)